

A tree is a graph in which any two nodes are connected by at least one path or edge, as illustrated below. Each edge may have a weight which might represent the distance between nodes.
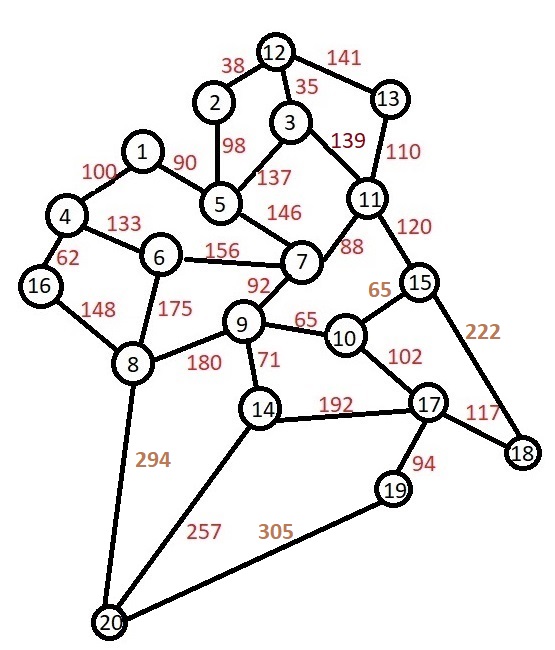
First, let's create classes for Node and Edge and then combine these to create a Graph class.
First, the Node class.
using System.Collections.Generic;
namespace Graphs
{
public class Node
{
public int Index { get; set; }
public T Data { get; set; }
public List> Neighbors { get; set; } = new List>();
public List Weights { get; set; } = new List();
public override string ToString()
{
return $"Node {NodeData}, connected to {Neighbors.Count} neighbor(s)";
}
}
}
Now the Edge class.
namespace Graphs
{
public class Edge
{
public Node From { get; set; }
public Node To { get; set; }
public int Weight { get; set; }
public override string ToString()
{
return $"Edge: {From.Data} -> {To.Data}, weight: {Weight}";
}
}
}
Now let's add a Graph class.
using System.Collections.Generic;
namespace Graphs
{
public class Graph
{
private bool _isDirected = false;
private bool _isWeighted = false;
public List> Nodes { get; set; } = new List>();
public Edge this[int from, int to]
{
get
{
Node nodeFrom = Nodes[from];
Node nodeTo = Nodes[to];
int i = nodeFrom.Neighbors.IndexOf(nodeTo);
if (i >= 0)
{
Edge edge = new Edge()
{
From = nodeFrom,
To = nodeTo,
Weight = i < nodeFrom.Weights.Count ? nodeFrom.Weights[i] : 0
};
return edge;
}
return null;
}
}
public Graph(bool isDirected, bool isWeighted)
{
_isDirected = isDirected;
_isWeighted = isWeighted;
}
public Node AddNode(T value)
{
Node node = new Node() { Data = value };
Nodes.Add(node);
UpdateIndices();
return node;
}
public void AddEdge(Node from, Node to, int weight = 0)
{
from.Neighbors.Add(to);
if (_isWeighted)
{
from.Weights.Add(weight);
}
if (!_isDirected)
{
to.Neighbors.Add(from);
if (_isWeighted)
{
to.Weights.Add(weight);
}
}
}
public void RemoveNode(Node nodeToRemove)
{
Nodes.Remove(nodeToRemove);
UpdateIndices();
foreach (Node node in Nodes)
{
RemoveEdge(node, nodeToRemove);
}
}
public void RemoveEdge(Node from, Node to)
{
int index = from.Neighbors.FindIndex(n => n == to);
if (index >= 0)
{
from.Neighbors.RemoveAt(index);
from.Weights.RemoveAt(index);
}
}
public List> GetEdges()
{
List> edges = new List>();
foreach (Node from in Nodes)
{
for (int i = 0; i < from.Neighbors.Count; i++)
{
Edge edge = new Edge()
{
From = from,
To = from.Neighbors[i],
Weight = i < from.Weights.Count ? from.Weights[i] : 0
};
edges.Add(edge);
}
}
return edges;
}
private void UpdateIndices()
{
int i = 0;
Nodes.ForEach(n => n.Index = i++);
}
}
}
We would like to traverse the graph by visiting each node. First we will show two ways to perform an "uninformed search" by examining nodes by depth (Depth First Search) and then by breadth (Breadth FirstSearch).
First, a Depth First Search using the previous graph.
// Depth First Search
public static List> DepthFirstSearch(Graph graph)
{
int count = graph.Nodes.Count;
bool[] isVisited = new bool[count];
List> result = new List>();
DepthFirstSearch(isVisited, graph.Nodes[0], result);
return result;
}
private static void DepthFirstSearch(bool[] isExplored, Node node, List> result)
{
result.Add(node);
isExplored[node.Index] = true;
foreach (Node neighbor in node.Neighbors)
{
if (!isExplored[neighbor.Index])
{
DepthFirstSearch(isExplored, neighbor, result);
}
}
}
This produces the following list of nodes and number of connections to other nodes that each node has.
Node 1, connected to 2 neighbor(s) Node 4, connected to 3 neighbor(s) Node 6, connected to 3 neighbor(s) Node 7, connected to 4 neighbor(s) Node 5, connected to 4 neighbor(s) Node 2, connected to 2 neighbor(s) Node 12, connected to 3 neighbor(s) Node 3, connected to 3 neighbor(s) Node 11, connected to 4 neighbor(s) Node 13, connected to 2 neighbor(s) Node 15, connected to 3 neighbor(s) Node 10, connected to 3 neighbor(s) Node 9, connected to 4 neighbor(s) Node 8, connected to 4 neighbor(s) Node 16, connected to 2 neighbor(s) Node 20, connected to 3 neighbor(s) Node 14, connected to 3 neighbor(s) Node 17, connected to 3 neighbor(s) Node 18, connected to 2 neighbor(s) Node 19, connected to 2 neighbor(s)